浅谈回溯算法及其相关优化方法和Best First Search扩展
在看回溯算法的时候有看到这个概念,就查询了一下网上的资料,发现都是一些形式化的概念,今天我就按照我的理解简述一下这个算法策略以及其相关内容吧。
注:本文中所有提到的BFS均指的是Best First Search不是宽度优先遍历
1.回溯算法
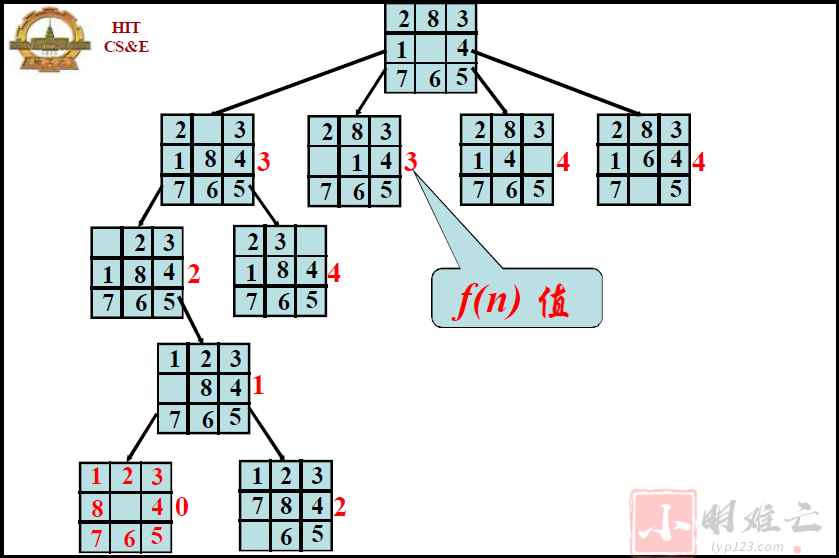
这个是最基础的搜索算法,也是对解空间的暴力搜索算法,举个栗子,8-Puzzle问题,类似于魔方,将所有的情况都转化为终点情况,回溯就是暴力枚举所有的解,如下图所示:
2.爬山策略
需要理解BFS之前,咱们先来看看爬山策略,这个策略就是按照上面的算法进行的优化,核心就是如何理解这个爬山比较,按照下图所示,可以设置一个函数对于每一个状态设置一个函数计算当前状态距离最终状态的距离,通过搜索比较当前函数值的最优值确定搜索方向,继续往下搜索,直到得出解或者是到达搜索终点,结束算法。该策略结合深度优先和广度优先的优点,根据一个评价函数, 在目前产生的所有节点中选择具有最小评价函数值的节点进行扩展,仅具有局部优化观念。
用更加形式化的语言定义:这就是在每一状态下都选取这样的步骤进行试探:由这个步骤所达到的终结状态是所有可容许步骤所能达到的终结状态中,最接近最终目标的一个。这样的步骤称为最优步骤。按照这样的原则依次选取步骤,顺序试探下去,直到最终目标为止。如果达不到最终目标,可以回过头来,从已经经历过的某一中间状态开始,改用直接效果稍差一点的次优步骤,沿着另一条分支途径再行试探下去。当然,也可以一下子回转到整个问题的起始状态,沿着另一条全新的途径进行试探。到底应当返回到什么状态开始另行试探,这要由解题者根据具体情况作出自己的判断。
爬山法:
3.Best First Search
这里相比于爬山法的区别就是,爬山法是的评价函数是针对当前的状态评价下一步,而BFS是使用当前状态到终点的距离判断来判断下一步该往哪里走,当然也可以设置为当前的状态,这看解题者如何处理这个函数了。这个BFS可以使用在单源最短路中,由于其局部优化的观念,导致可能不是最优解,但是在要求精度不高的情况下换来的是时间很快。
Best First Search:
4.分支界限策略
理解了上面那两个策略以后,咱立马用起来,首先使用上面的策略产生分支,然后根据代价矩阵或者代价评价函数计算界限,这个界限指的是不可能继续优化的界限,防止不可继续优化而继续优化的计算资源浪费,将不可继续优化的分支裁剪掉,不再继续扩展下去。
5.A*算法
这里是一点扩展内容,大家应该都知道dijkstra算法,是计算单源最短路的公认的方法,但是有时候计算时间也就是时间复杂度还是比较高的,而BFS速度比较快,A*就是这两种方法的结合体,设计一个评价函数F(x)= a(x)+ b(x),a(x)为起点到当前点的最短路径也就是dijkstra算法的计算公式,而b(x)指的是当前点到终点的距离评价函数,综合F(x)是总评价函数,作为下一个扩展点的评价函数,可以加快dijkstra算法的速度和BFS的精确度,可以说是比较均衡的算法,在实际应用中使用范围很广,是一个人工智能搜索算法。
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可。



 微信
微信
 支付宝
支付宝
到此一游